How to create 2D triangle ?
OpenLB – Open Source Lattice Boltzmann Code › Forums › on OpenLB › General Topics › How to create 2D triangle ?
- This topic has 17 replies, 3 voices, and was last updated 2 years, 8 months ago by mathias.
-
AuthorPosts
-
October 25, 2021 at 11:15 am #6094FanyParticipant
Hi everyone,
I want to create some 2D triangles but there is no IndicatorF for triangles like IndicatorCuboid2D for cubiods. Do you know how to do that?
I found there is a functor called SmoothIndicatorTriangle2D but what do the mass, epsilon and theta in that functor mean? The “SmoothXXX” one seems to be different from the general IndicatorF like IndicatorCuboid2D. What does “Smooth” stand for? Thank you.
October 26, 2021 at 8:59 pm #6104AdrianKeymasterDoesIndicatorTriangle2Dfullfill your requirements?This will be available in the next release. Ordinarily I’d quickly backport it to 1.4 for you but the new indicator is tied to more comprehensive changes of the library and unfortunately not easy to extract.
In general, smooth indicators are used by the resolved particle code to model particles with a porous boundary layer (in HLBM). See e.g.
R. Trunk et al. “Towards the Simulation of arbitrarily shaped 3D particles using a homogenised lattice Boltzmann method”. In: Computers & Fluids 172 (2018). doi: https://doi.org/10.1016/j.compfluid.2018.02.027.
October 27, 2021 at 8:47 am #6112FanyParticipantHi Adrian,
Glad to hear the new release. By the way, in the present vision 1.4, Does the parallelepiped version of creating a 2D cuboid achieve by setting the parameter Theta? If does, the the code below should include the parameter theta?
template <typename S> IndicatorCuboid2D<S>::IndicatorCuboid2D(S xLength, S yLength, Vector<S,2> center, S theta ) : _center(center), _xLength(xLength), _yLength(yLength), _theta(-theta) { this->_myMin = {_center[0] - _xLength/2., _center[1] - _yLength/2.}; this->_myMax = {_center[0] + _xLength/2., _center[1] + _yLength/2.}; }October 28, 2021 at 7:29 pm #6117FanyParticipantHi Adrian, I am creating the 2D triangle and cuboid without parallel to the X=0 and Y=0. But the computation with my geometry diverged. Could you please help check what the problems with the code below are?
// creating the cuboid with the theta of rotation around its center template <typename S> IndicatorCuboid2D<S>::IndicatorCuboid2D(S xLength, S yLength, Vector<S,2> center, S theta ) : _center(center), _xLength(xLength), _yLength(yLength), _theta(theta) { if (_theta>=0 && _theta <= M_PI2){ this->_myMin = {_center[0] - (_xLength*std::cos(_theta)/2.+_yLength*std::sin(_theta)/2.), _center[1] - (_yLength*std::cos(_theta)/2.+_xLength*std::sin(_theta)/2.) }; this->_myMax = {_center[0] + (_xLength*std::cos(_theta)/2.+_yLength*std::sin(_theta)/2.), _center[1] + (_yLength*std::cos(_theta)/2.+_xLength*std::sin(_theta)/2.) }; } if (_theta>=-M_PI2 && _theta < 0){ this->_myMin = {_center[0] - (_xLength*std::cos(_theta)/2.-_yLength*std::sin(_theta)/2.), _center[1] - (_yLength*std::cos(_theta)/2.-_xLength*std::sin(_theta)/2.) }; this->_myMax = {_center[0] + (_xLength*std::cos(_theta)/2.-_yLength*std::sin(_theta)/2.), _center[1] + (_yLength*std::cos(_theta)/2.-_xLength*std::sin(_theta)/2.)}; } } template <typename S> bool IndicatorCuboid2D<S>::operator()(bool output[], const S input[]) { S x, y; if ( !util::nearZero(_theta) ) { x = _center[0] + (input[0] - _center[0])*std::cos(_theta) + (input[1] - _center[1])*std::sin(_theta); y = _center[1] + (input[1] - _center[1])*std::cos(_theta) - (input[0] - _center[0])*std::sin(_theta); } else { x = input[0]; y = input[1]; } output[0] = ( (fabs(_center[0] - x) < _xLength/2. || util::approxEqual(fabs(_center[0] - x),_xLength/2.) ) && (fabs(_center[1] - y) < _yLength/2. || util::approxEqual(fabs(_center[1] - y), _yLength/2.) ) ); return true; } // creating the triangle template <typename S> IndicatorTriangle2D<S>::IndicatorTriangle2D(Vector<S,2> PointA, Vector<S,2> PointB, Vector<S,2> PointC) : _PointA(PointA), _PointB(PointB), _PointC(PointC) { this->_myMin = { std::min(_PointA[0], std::min(_PointB[0], _PointC[0])), std::min(_PointA[1], std::min(_PointB[1], _PointC[1]))}; this->_myMax = { std::max(_PointA[0], std::max(_PointB[0], _PointC[0])), std::max(_PointA[1], std::max(_PointB[1], _PointC[1]))}; _ab = _PointB - _PointA; _bc = _PointC - _PointB; _ca = _PointA - _PointC; } template <typename S> bool IndicatorTriangle2D<S>::operator()(bool output[], const S input[]) { Vector<S, 2> _Point ; _Point[0] = input[0]; _Point[1] = input[1]; //any point M Vector<S, 2> _am=_Point - _PointA ; Vector<S, 2> _bm=_Point - _PointB ; Vector<S, 2> _cm=_Point - _PointC ; S S_ABM = fabs(_ab[1]*_am[0]-_ab[0]*_am[1])/2. ; // the area of triangle ABM; S S_BCM = fabs(_bc[1]*_bm[0]-_ca[0]*_bm[1])/2. ; // the area of triangle BCM; S S_CAM = fabs(_ca[1]*_cm[0]-_ca[0]*_cm[1])/2. ; // the area of triangle CAM; S Sum = fabs(_ca[1]*_ab[0]-_ca[0]*_ab[1])/2. ; // the area of triangle CAM; output[0] = util::approxEqual(S_ABM + S_BCM + S_CAM,Sum) ; return true; }November 2, 2021 at 1:23 pm #6139AdrianKeymasterSo the simulation worked with a different indicator? Do the material numbers look as expected (you can check in ParaView)? Which boundary conditions and bulk dynamics are you using? If you inspect the results prior to divergence, where do the problems originate from?
November 2, 2021 at 3:01 pm #6144FanyParticipantYes, I created a new indicator for triangle and inclined rectangle, but i don’t know why there is a problem in setting the outlet materials for inclined rectangle and how to clean the unnecessary voxels outside, as following:
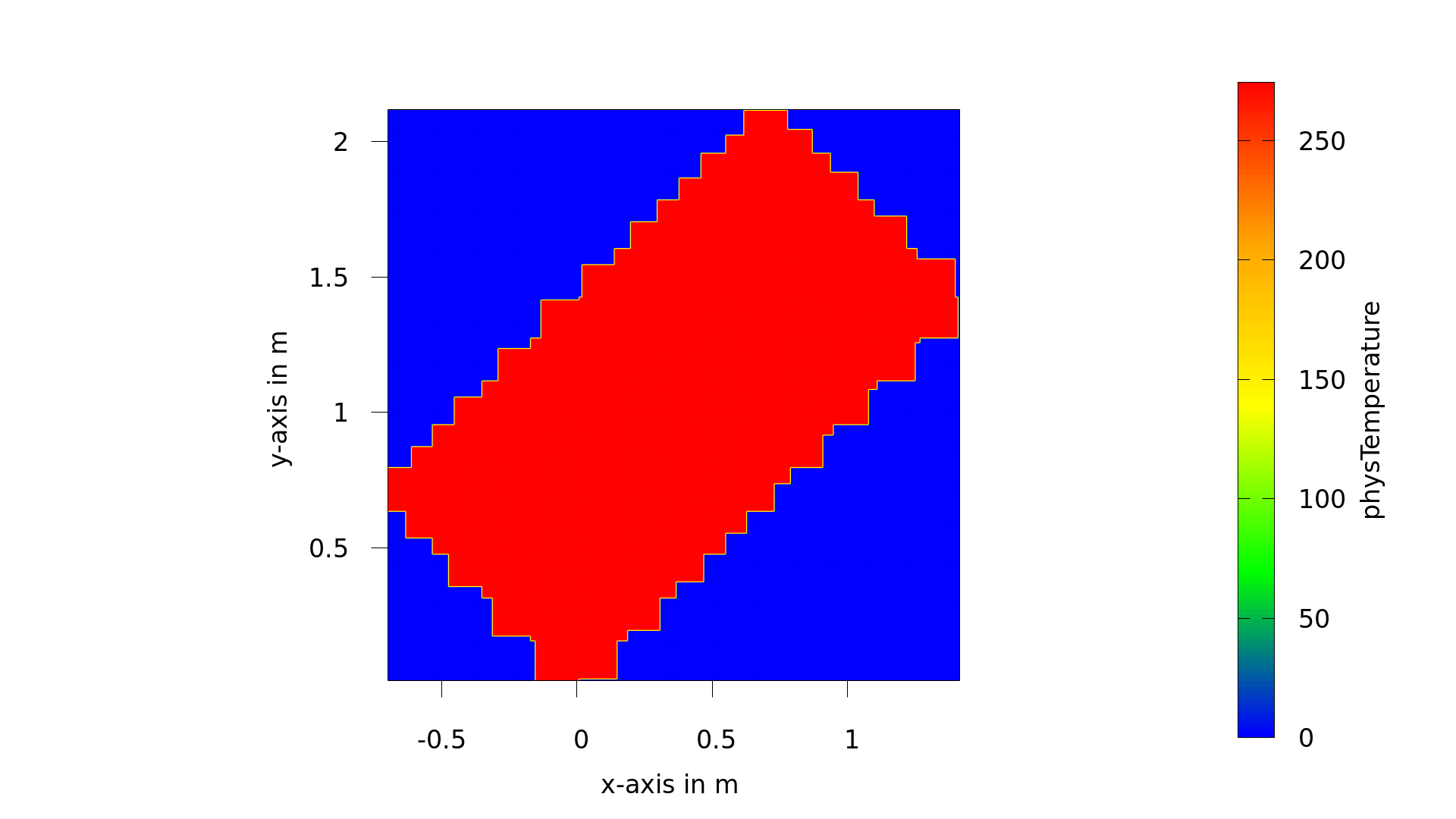
The statistic of outflow material number (another geometry of inclined rectangle) was 1-fluid, 2-boundary, 3-inflow, 4-outflow:
`[SuperGeometryStatistics2D]materialNumber=1; count=18848; minPhysR=(-0.00148286,-0.00185643); maxPhysR=(0.00324857,0.00186357)
[SuperGeometryStatistics2D] materialNumber=2; count=1066; minPhysR=(-0.0015,-0.00187357); maxPhysR=(0.00326571,0.00188072)
[SuperGeometryStatistics2D] materialNumber=3; count=45; minPhysR=(-0.0015,-0.000382141); maxPhysR=(-0.0015,0.000372145)
[SuperGeometryStatistics2D] materialNumber=4; count=3; minPhysR=(0.00321429,0.00148643); maxPhysR=(0.00326571,0.00153786)November 3, 2021 at 2:33 pm #6147AdrianKeymasterThis looks as if the inclined rectangle intersects the domain boundaries which likely interferes with the setup. I would also suggest to increase the resolution as I would be surprised if you got sensible results for this rough a setup.
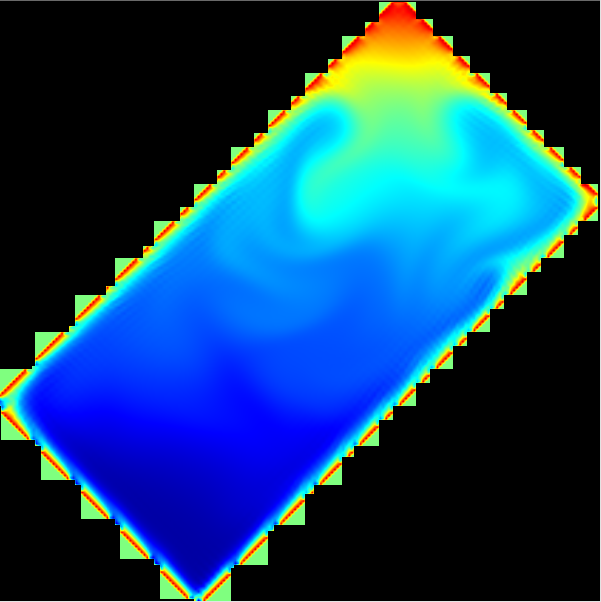
November 3, 2021 at 3:00 pm #6151FanyParticipantIt is not resolution but the number of cuboids ( by CuboidGeometry). You can see the following image.
 November 3, 2021 at 3:10 pm #6152AdrianKeymaster
November 3, 2021 at 3:10 pm #6152AdrianKeymasterOk – in this case there is definitely something weird going on as the rectangle intersects the cuboids and these intersections are also where the divergence seems to come from. What happens if you use only one cuboid (as a minimal case)? (In any case: For such a low resolution it likely doesn’t make sense to increase the cuboid number to the degree that it is done here)
Not directly related: What is the reason for inclining the rectangle if you only simulate inside it anyway?
- This reply was modified 2 years, 8 months ago by Adrian.
November 3, 2021 at 3:22 pm #6154FanyParticipantGood, thanks. I will try to increase the resolution. But I found the resolution in the examples of OpenLB library seemed to be usually set at 10-35. In my case, the resolution was set at 10 (same with that in rayleiBenard2d case).
By the way, the inclined rectangle above was just obtained by rotating the rectangle of rayleiBenard2d case (OpenLB) for 45°. The blue area above should be the unnecessary part outside of the rectangle?November 3, 2021 at 5:37 pm #6155FanyParticipantI am trying to simulate the flow heat transfer in a inclined pipe (2D)
November 8, 2021 at 10:32 am #6159AdrianKeymasterw.r.t. resolution: The
Nconstant (which as you say is commonly between 10 – 35) is only a useful proxy for the actual resolution that results of the spatial discretization delta and the domain size. This delta is computed by dividing some reference length (chosen to fit what is modeled by each simulation case) divided by theNconstant.w.r.t. inclined geometry / pipe: If my understanding of what you want to simulate is correct, you would be better served to keep the geometry axis aligned s.t. it is nicely discretized by the regular grid and model the inclination by rotating the external force field. This also should get rid of the cuboid decomposition problems (which point to some issue in domain setup).
November 10, 2021 at 6:51 pm #6166FanyParticipantHi Adrian, I was creating the 2D triangle by my own triangle functor. But the visualization result showed my functor did not work. What could be the problems here? By the way, when will the next release be ?
`
// creating the triangle
template <typename S>
IndicatorTriangle2D<S>::IndicatorTriangle2D(Vector<S,2> PointA, Vector<S,2> PointB, Vector<S,2> PointC)
: _PointA(PointA), _PointB(PointB), _PointC(PointC)
{
// S AB=std::sqrt(std::pow(_PointB[0]-_PointA[0], 2)+std::pow(_PointB[1]-_PointA[1], 2));
// S AC=std::sqrt(std::pow(_PointC[0]-_PointA[0], 2)+std::pow(_PointC[1]-_PointA[1], 2));
// S BC=std::sqrt(std::pow(_PointB[0]-_PointC[0], 2)+std::pow(_PointB[1]-_PointC[1], 2));
// S halfperi=0.5*(AB+AC+BC);
// S temp=halfperi*(halfperi-AB)*(halfperi-AC)*(halfperi-BC);
// this->_circumRadius = 0.25*AB*AC*BC/std::sqrt(temp);this->_myMin = { std::min(_PointA[0], std::min(_PointB[0], _PointC[0])), std::min(_PointA[1], std::min(_PointB[1], _PointC[1]))};
this->_myMax = { std::max(_PointA[0], std::max(_PointB[0], _PointC[0])), std::max(_PointA[1], std::max(_PointB[1], _PointC[1]))};
// this->_theta = theta * M_PI/180.;_ab = _PointB – _PointA;
_bc = _PointC – _PointB;
_ca = _PointA – _PointC;}
template <typename S>
bool IndicatorTriangle2D<S>::operator()(bool output[], const S input[])
{
Vector<S, 2> _Point ;
_Point[0] = input[0];
_Point[1] = input[1]; //any point M
Vector<S, 2> _am=_Point – _PointA ;
Vector<S, 2> _bm=_Point – _PointB ;
Vector<S, 2> _cm=_Point – _PointC ;S S_ABM = fabs(_ab[1]*_am[0]-_ab[0]*_am[1])/2. ; // the area of triangle ABM;
S S_BCM = fabs(_bc[1]*_bm[0]-_ca[0]*_bm[1])/2. ; // the area of triangle BCM;
S S_CAM = fabs(_ca[1]*_cm[0]-_ca[0]*_cm[1])/2. ; // the area of triangle CAM;
S Sum = fabs(_ca[1]*_ab[0]-_ca[0]*_ab[1])/2. ; // the area of triangle CAM;output[0] = util::approxEqual(S_ABM + S_BCM + S_CAM, Sum) ;
return true;
}template <typename S>
IndicatorTriangle2D<S>* createIndicatorTriangle2D(XMLreader const& params, bool verbose)
{
OstreamManager clout(std::cout,”createIndicatorTriangle2D”);
params.setWarningsOn(verbose);Vector<S,2> PointA;
Vector<S,2> PointB;
Vector<S,2> PointC;std::stringstream xmlCenter( params.getAttribute(“PointA”) );
xmlCenter >> PointA[0] >> PointA[1]>> PointB[0] >> PointB[1]>> PointC[0] >> PointC[1];// std::stringstream xmlRadius( params.getAttribute(“length”) );
// xmlRadius >> xLength >> yLength;return new IndicatorCuboid2D<S>(PointA, PointB, PointC);
}November 11, 2021 at 10:38 pm #6168AdrianKeymasterThe next release is planned for sometime in the first half of 2022 (we realize that it already has been quite a while since the last release, however the next release will be worth the wait in more than one aspect… :-))
Your indicator class looks ok at first glance but I am afraid that we can not provide general C++ programming support here. Did you check it in a minimal example (i.e. without XML, as simple as you can make it). If you satisfy the basic indicator interface
operator()(bool output[], const S input[])then everything downstream should work.November 12, 2021 at 2:18 pm #6171FanyParticipantThat is great, really looking forward to the new release.
I change the way to creating the geometry, but I have a question of how to deal with BC. I found that the inclined boundary just had 3-4 voxels (but the resolution was actually 35), and the BC was determined by a thin inclined rectangle. I referred to the example “aorta3d”. as following:

-
AuthorPosts
- You must be logged in to reply to this topic.
