Fany
Forum Replies Created
-
AuthorPosts
-
FanyParticipant
Hello Anand,
Do you test OpenLB 1.5. I ran my case in the OpenLB v1.5, and it always occurred the segmentation faults. But it can work in OpenLB 1.4.
Thanks for your attention.FanyParticipantHi Adrian,
Thanks for your recommendation. But I have to incline a 2d cuboid of the whole geometry, which was created by 2 cubiod (one is parallel to the axis, the other has to be inclined). That geometry was similar to the example aorta3d model.
In my case, the deltaX was equal to the width of the inclined cuboid dividing the resolution N (35). I do not know why the number of outflow materials was just 3 when setting the inclined outlet, while the vertical outlet was normal.
 FanyParticipant
FanyParticipantThat is great, really looking forward to the new release.
I change the way to creating the geometry, but I have a question of how to deal with BC. I found that the inclined boundary just had 3-4 voxels (but the resolution was actually 35), and the BC was determined by a thin inclined rectangle. I referred to the example “aorta3d”. as following:
 FanyParticipant
FanyParticipantHi Adrian, I was creating the 2D triangle by my own triangle functor. But the visualization result showed my functor did not work. What could be the problems here? By the way, when will the next release be ?
`
// creating the triangle
template <typename S>
IndicatorTriangle2D<S>::IndicatorTriangle2D(Vector<S,2> PointA, Vector<S,2> PointB, Vector<S,2> PointC)
: _PointA(PointA), _PointB(PointB), _PointC(PointC)
{
// S AB=std::sqrt(std::pow(_PointB[0]-_PointA[0], 2)+std::pow(_PointB[1]-_PointA[1], 2));
// S AC=std::sqrt(std::pow(_PointC[0]-_PointA[0], 2)+std::pow(_PointC[1]-_PointA[1], 2));
// S BC=std::sqrt(std::pow(_PointB[0]-_PointC[0], 2)+std::pow(_PointB[1]-_PointC[1], 2));
// S halfperi=0.5*(AB+AC+BC);
// S temp=halfperi*(halfperi-AB)*(halfperi-AC)*(halfperi-BC);
// this->_circumRadius = 0.25*AB*AC*BC/std::sqrt(temp);this->_myMin = { std::min(_PointA[0], std::min(_PointB[0], _PointC[0])), std::min(_PointA[1], std::min(_PointB[1], _PointC[1]))};
this->_myMax = { std::max(_PointA[0], std::max(_PointB[0], _PointC[0])), std::max(_PointA[1], std::max(_PointB[1], _PointC[1]))};
// this->_theta = theta * M_PI/180.;_ab = _PointB – _PointA;
_bc = _PointC – _PointB;
_ca = _PointA – _PointC;}
template <typename S>
bool IndicatorTriangle2D<S>::operator()(bool output[], const S input[])
{
Vector<S, 2> _Point ;
_Point[0] = input[0];
_Point[1] = input[1]; //any point M
Vector<S, 2> _am=_Point – _PointA ;
Vector<S, 2> _bm=_Point – _PointB ;
Vector<S, 2> _cm=_Point – _PointC ;S S_ABM = fabs(_ab[1]*_am[0]-_ab[0]*_am[1])/2. ; // the area of triangle ABM;
S S_BCM = fabs(_bc[1]*_bm[0]-_ca[0]*_bm[1])/2. ; // the area of triangle BCM;
S S_CAM = fabs(_ca[1]*_cm[0]-_ca[0]*_cm[1])/2. ; // the area of triangle CAM;
S Sum = fabs(_ca[1]*_ab[0]-_ca[0]*_ab[1])/2. ; // the area of triangle CAM;output[0] = util::approxEqual(S_ABM + S_BCM + S_CAM, Sum) ;
return true;
}template <typename S>
IndicatorTriangle2D<S>* createIndicatorTriangle2D(XMLreader const& params, bool verbose)
{
OstreamManager clout(std::cout,”createIndicatorTriangle2D”);
params.setWarningsOn(verbose);Vector<S,2> PointA;
Vector<S,2> PointB;
Vector<S,2> PointC;std::stringstream xmlCenter( params.getAttribute(“PointA”) );
xmlCenter >> PointA[0] >> PointA[1]>> PointB[0] >> PointB[1]>> PointC[0] >> PointC[1];// std::stringstream xmlRadius( params.getAttribute(“length”) );
// xmlRadius >> xLength >> yLength;return new IndicatorCuboid2D<S>(PointA, PointB, PointC);
}FanyParticipantI am trying to simulate the flow heat transfer in a inclined pipe (2D)
FanyParticipantGood, thanks. I will try to increase the resolution. But I found the resolution in the examples of OpenLB library seemed to be usually set at 10-35. In my case, the resolution was set at 10 (same with that in rayleiBenard2d case).
By the way, the inclined rectangle above was just obtained by rotating the rectangle of rayleiBenard2d case (OpenLB) for 45°. The blue area above should be the unnecessary part outside of the rectangle?FanyParticipantIt is not resolution but the number of cuboids ( by CuboidGeometry). You can see the following image.
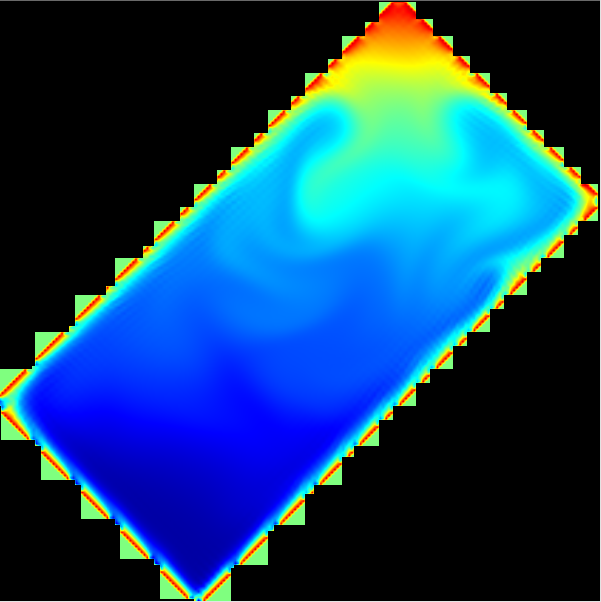 FanyParticipant
FanyParticipantYes, I created a new indicator for triangle and inclined rectangle, but i don’t know why there is a problem in setting the outlet materials for inclined rectangle and how to clean the unnecessary voxels outside, as following:
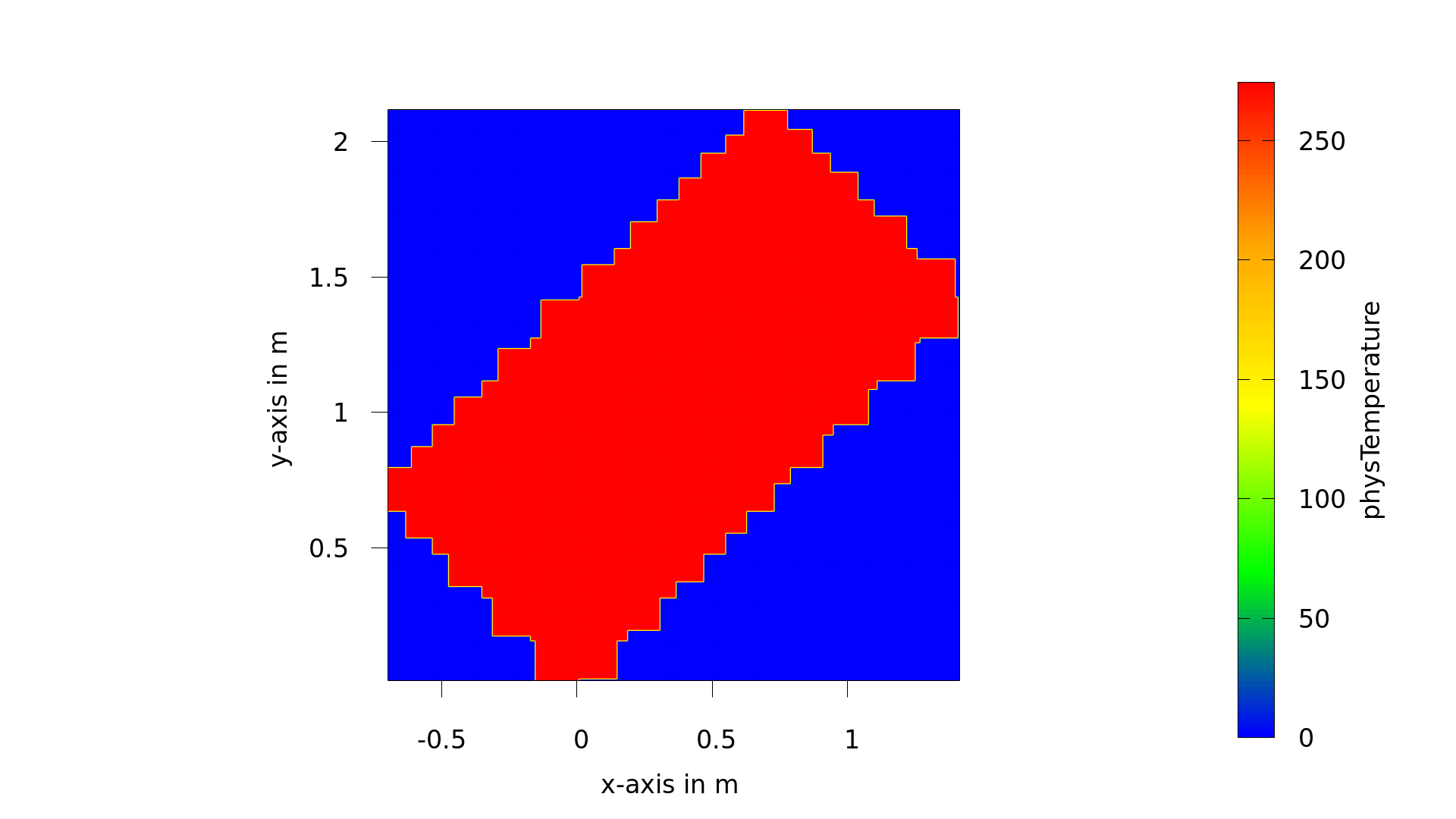
The statistic of outflow material number (another geometry of inclined rectangle) was 1-fluid, 2-boundary, 3-inflow, 4-outflow:
`[SuperGeometryStatistics2D]materialNumber=1; count=18848; minPhysR=(-0.00148286,-0.00185643); maxPhysR=(0.00324857,0.00186357)
[SuperGeometryStatistics2D] materialNumber=2; count=1066; minPhysR=(-0.0015,-0.00187357); maxPhysR=(0.00326571,0.00188072)
[SuperGeometryStatistics2D] materialNumber=3; count=45; minPhysR=(-0.0015,-0.000382141); maxPhysR=(-0.0015,0.000372145)
[SuperGeometryStatistics2D] materialNumber=4; count=3; minPhysR=(0.00321429,0.00148643); maxPhysR=(0.00326571,0.00153786)November 1, 2021 at 10:44 am in reply to: How to create the cuboidGeometry for a inclined 2D cuboid geometry #6130FanyParticipantHi Gloriousface,
Here is the code of renaming the material numbers.
`
OstreamManager clout(std::cout,”prepareGeometry”);
clout << “Prepare Geometry …” << std::endl;superGeometry.rename(0,2);
superGeometry.rename(2,1,0,1);std::vector<T> extend( 2, T(0) );
extend[0] = lx;
extend[1] = converter.getPhysLength(1);
std::vector<T> origin( 2, T(0) );
IndicatorCuboid2D<T> bottom(extend, origin, theta);origin[1] = ly-converter.getPhysLength(1);
IndicatorCuboid2D<T> top(extend, origin, theta);origin[0] = lx/2.;
origin[1] = converter.getPhysLength(1);
extend[0] = converter.getPhysLength(1);
extend[1] = converter.getPhysLength(1);
IndicatorCuboid2D<T> perturbation(extend, origin, theta);/// Set material numbers for bottom, top and pertubation
superGeometry.rename(2,2,1,bottom);
superGeometry.rename(2,3,1,top);
superGeometry.rename(1,4,perturbation);/// Removes all not needed boundary voxels outside the surface
superGeometry.clean();
/// Removes all not needed boundary voxels inside the surface
superGeometry.innerClean();
superGeometry.checkForErrors();superGeometry.print();
clout << “Prepare Geometry … OK” << std::endl;
November 1, 2021 at 10:40 am in reply to: How to create the cuboidGeometry for a inclined 2D cuboid geometry #6129FanyParticipantDear Gloriousface,
Thanks very much for your suggestion of creating the geometry boundary. Is that used to rename the boundary but not using the class supergeometry.rename in OpenLB?
Actually, I feel the serrated boundary was caused by the class CuboidGeometry2D because the boundary would changed with the different parameter noofCuboids and increasingly approximate to a rectangle with the increasing noofcuboids. I mean the problem may occurred in the process of constructing cuboid, shrinking remaining cuboids, distributing the load balancer and renaming material. I adapted the functor IndicatorCuboid2D to creating the 2D cuboid with a rotation angle. But it is normal when the angle=90, but abnormal when the angle was 45 (seen in the above image).`/// === 2nd Step: Prepare Geometry ===
std::vector<T> extend(2,T());
extend[0] = lx;
extend[1] = ly;
std::vector<T> origin(2,T());
IndicatorCuboid2D<T> cuboid(extend, origin, theta);/// Instantiation of a cuboidGeometry with weights
#ifdef PARALLEL_MODE_MPI
const int noOfCuboids = 16*singleton::mpi().getSize();
#else
const int noOfCuboids = 7;
#endif
CuboidGeometry2D<T> cuboidGeometry(cuboid, converter.getPhysDeltaX(), noOfCuboids);// cuboidGeometry.setPeriodicity(true, false);
HeuristicLoadBalancer<T> loadBalancer(cuboidGeometry);
SuperGeometry2D<T> superGeometry(cuboidGeometry, loadBalancer, 2);
prepareGeometry(superGeometry, converter);
FanyParticipantHi Adrian, I am creating the 2D triangle and cuboid without parallel to the X=0 and Y=0. But the computation with my geometry diverged. Could you please help check what the problems with the code below are?
// creating the cuboid with the theta of rotation around its center template <typename S> IndicatorCuboid2D<S>::IndicatorCuboid2D(S xLength, S yLength, Vector<S,2> center, S theta ) : _center(center), _xLength(xLength), _yLength(yLength), _theta(theta) { if (_theta>=0 && _theta <= M_PI2){ this->_myMin = {_center[0] - (_xLength*std::cos(_theta)/2.+_yLength*std::sin(_theta)/2.), _center[1] - (_yLength*std::cos(_theta)/2.+_xLength*std::sin(_theta)/2.) }; this->_myMax = {_center[0] + (_xLength*std::cos(_theta)/2.+_yLength*std::sin(_theta)/2.), _center[1] + (_yLength*std::cos(_theta)/2.+_xLength*std::sin(_theta)/2.) }; } if (_theta>=-M_PI2 && _theta < 0){ this->_myMin = {_center[0] - (_xLength*std::cos(_theta)/2.-_yLength*std::sin(_theta)/2.), _center[1] - (_yLength*std::cos(_theta)/2.-_xLength*std::sin(_theta)/2.) }; this->_myMax = {_center[0] + (_xLength*std::cos(_theta)/2.-_yLength*std::sin(_theta)/2.), _center[1] + (_yLength*std::cos(_theta)/2.-_xLength*std::sin(_theta)/2.)}; } } template <typename S> bool IndicatorCuboid2D<S>::operator()(bool output[], const S input[]) { S x, y; if ( !util::nearZero(_theta) ) { x = _center[0] + (input[0] - _center[0])*std::cos(_theta) + (input[1] - _center[1])*std::sin(_theta); y = _center[1] + (input[1] - _center[1])*std::cos(_theta) - (input[0] - _center[0])*std::sin(_theta); } else { x = input[0]; y = input[1]; } output[0] = ( (fabs(_center[0] - x) < _xLength/2. || util::approxEqual(fabs(_center[0] - x),_xLength/2.) ) && (fabs(_center[1] - y) < _yLength/2. || util::approxEqual(fabs(_center[1] - y), _yLength/2.) ) ); return true; } // creating the triangle template <typename S> IndicatorTriangle2D<S>::IndicatorTriangle2D(Vector<S,2> PointA, Vector<S,2> PointB, Vector<S,2> PointC) : _PointA(PointA), _PointB(PointB), _PointC(PointC) { this->_myMin = { std::min(_PointA[0], std::min(_PointB[0], _PointC[0])), std::min(_PointA[1], std::min(_PointB[1], _PointC[1]))}; this->_myMax = { std::max(_PointA[0], std::max(_PointB[0], _PointC[0])), std::max(_PointA[1], std::max(_PointB[1], _PointC[1]))}; _ab = _PointB - _PointA; _bc = _PointC - _PointB; _ca = _PointA - _PointC; } template <typename S> bool IndicatorTriangle2D<S>::operator()(bool output[], const S input[]) { Vector<S, 2> _Point ; _Point[0] = input[0]; _Point[1] = input[1]; //any point M Vector<S, 2> _am=_Point - _PointA ; Vector<S, 2> _bm=_Point - _PointB ; Vector<S, 2> _cm=_Point - _PointC ; S S_ABM = fabs(_ab[1]*_am[0]-_ab[0]*_am[1])/2. ; // the area of triangle ABM; S S_BCM = fabs(_bc[1]*_bm[0]-_ca[0]*_bm[1])/2. ; // the area of triangle BCM; S S_CAM = fabs(_ca[1]*_cm[0]-_ca[0]*_cm[1])/2. ; // the area of triangle CAM; S Sum = fabs(_ca[1]*_ab[0]-_ca[0]*_ab[1])/2. ; // the area of triangle CAM; output[0] = util::approxEqual(S_ABM + S_BCM + S_CAM,Sum) ; return true; }FanyParticipantHi Adrian,
Glad to hear the new release. By the way, in the present vision 1.4, Does the parallelepiped version of creating a 2D cuboid achieve by setting the parameter Theta? If does, the the code below should include the parameter theta?
template <typename S> IndicatorCuboid2D<S>::IndicatorCuboid2D(S xLength, S yLength, Vector<S,2> center, S theta ) : _center(center), _xLength(xLength), _yLength(yLength), _theta(-theta) { this->_myMin = {_center[0] - _xLength/2., _center[1] - _yLength/2.}; this->_myMax = {_center[0] + _xLength/2., _center[1] + _yLength/2.}; }FanyParticipantYes, the problem still occurred by sequential mode. Thanks.
FanyParticipantHi Conglinfu,
Have you created the 2D triangle geometry? I am facing with the same problem. I don’t know why I can not open the link http://optilb.org/openlb/forum?mingleforumaction=viewtopic&t=247 and http://optilb.org/openlb/forum?mingleforumaction=viewtopic&t=249 which are found in the forum to be referred to create the geometry.FanyParticipantHi Adrian, the problem was solved by parallel computation. thanks. Presently, I want to build a triangle geometry. Can I refer to and adapt the SmoothIndicatorTriangle2D to do that?
-
AuthorPosts
